11. Composition of Homogeneous Transforms

Composition of Homogeneous Transforms

The composition of homogeneous transforms follows much the same logic as composition of rotations.

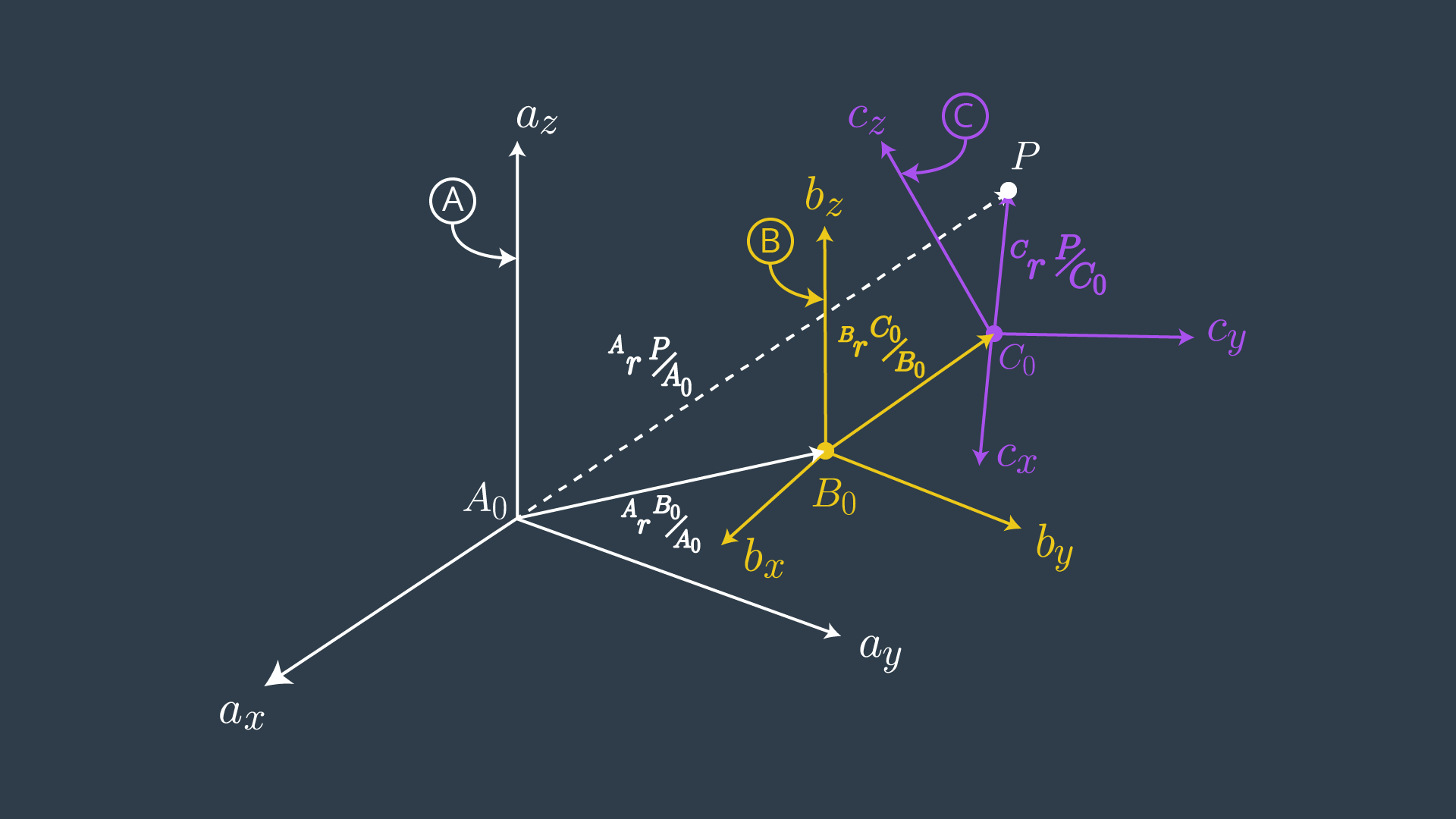
Assume the transform from frame C relative to frame B is known, as is the transform from B to A. It is possible then to express ^C\bold{r}{P/Co} in terms of frame _A by first transforming it to the frame B,

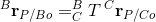
(1)

(1)

and then by transforming to the A frame,

(2)

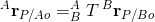
(2)

Perhaps not surprisingly, equations (1) and (2) can be combined as,

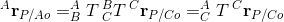
For completeness, let’s expand the transform between A and C in terms it’s known components,

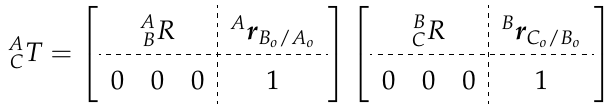
(3)

(3)

(4)

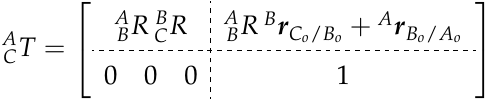
(4)

The upper left 3x3 submatrix in equation (4) should look familiar; it is a composition of rotations between A and C.

^A_BR \, ^B\bold{r}{Co/Bo} is the vector from B_o to C_o expressed in the _A frame. The final term, ^A\bold{r}{Bo/Ao}, is the vector from A_o to B_o expressed in _A.

To help solidify the concepts of transforms, inverse transforms, and composition of transforms, consider one more example. Here we have frames A through E.

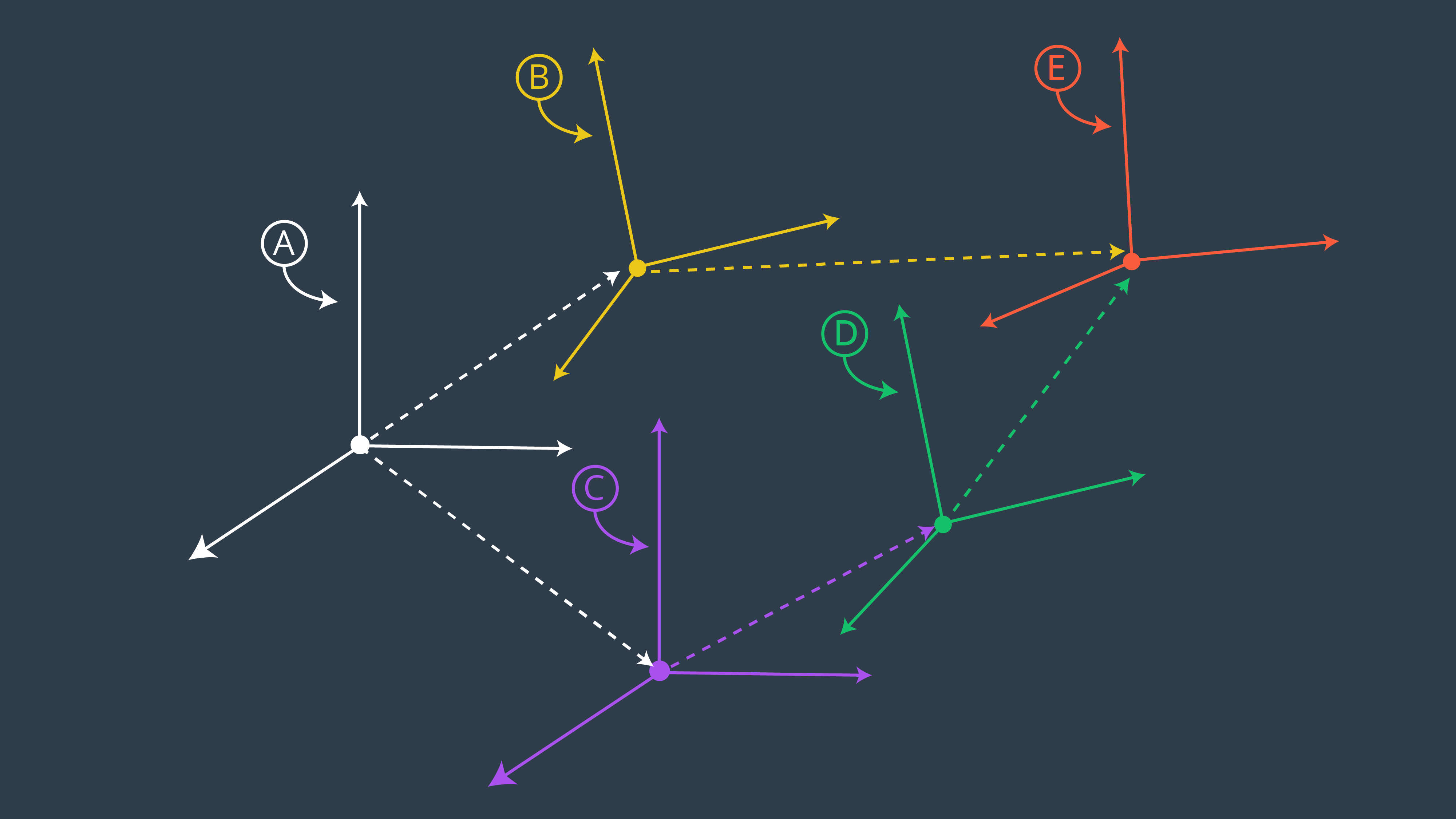
Let’s say we wish to create the transform between frames A and E; clearly, there are two paths. One route has transforms,

(5)

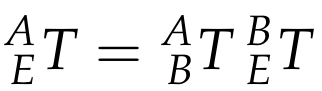
(5)

while the second is,

(6)

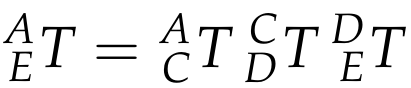
(6)

Equating (5) and (6) yields,

(7)

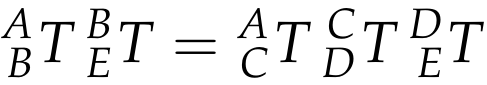
(7)

In the following Quiz, you will try to prove equation (7) and get some more experience with sympy. Refer to the image above. You will be implementing the transformations leading up to Frame E involving certain rotations and translations for each frame with respect to the previous frame.

The following steps are taken to obtain coordinate frame E from frame A.

From Frame A to B to E:

  • Frame A: Located at [0, 0, 0]
  • Frame B: Rotate Frame A about a_y by -90 degrees. Translate A by [-2, 2, 4]
  • Frame E: Rotate Frame B about b_x by 90 degrees. Translate B by [0, 2, 0]

From Frame A to C to D to E:

  • Frame C: Translate A by [4, 4, 0]
  • Frame D: Rotate Frame C about c_x by 90 degrees. Translate C by [-3, 3, 2]
  • Frame E: Rotate Frame D about d_Z by 90 degrees. Translate D by [-3, 2, 3]

Start Quiz:

#!/usr/bin/env python

from sympy import symbols, cos, sin, pi, sqrt, simplify
from sympy.matrices import Matrix

### Create symbols for joint variables
# The numbers 1 to 4 correspond to each rotation in the order specified to you.
q1, q2, q3, q4 = symbols('q1:5')

### Define functions for Rotation Matrices about x, y, and z given specific angle.

def rot_x(q):
    R_x = 0
    
    return R_x
    
def rot_y(q):              
    R_y = 0
    
    return R_y

def rot_z(q):    
    R_z = 0
    
    return R_z
              
### Define rotations between frames

# Initial Rotation Matrix for Frame A
Ra = Matrix([[1, 0, 0],
             [0, 1, 0],
             [0, 0, 1]])

# Rotations performed on individual Frames for A->B->E
Rb_a = 0
Re_b = 0

# Rotations performed on individual Frames for A->C->D->E
Rc_a = 0
Rd_c = 0
Re_d = 0

### Define Translations between frames.

tb_a = 0
te_b = 0
tc_a = 0
td_c = 0
te_d = 0

### Define homogenous transformation matrices
# HINT: Check out sympy's documentation for functions row_join and col_join
Ta = 0

Tb_a = 0

Te_b = 0

Tc_a = 0

Td_c = 0

Te_d = 0         

### Composition of Transformations
Te_a_1 = simplify(Ta * Tb_a * Te_b)

Te_a_2 = simplify(Ta * Tc_a * Td_c * Te_d)

### Calculate orientation and position for E
E_1 = Te_a_1.evalf(subs={q1: 0, q2: 0}, chop = True)

E_2 = Te_a_2.evalf(subs={q3: 0, q4: 0}, chop = True)

print("Transformation Matrix for A->B->E:")
print(E_1)

print("Transformation Matrix for A->C->D->E:")
print(E_2)



#!/usr/bin/env python

from sympy import symbols, cos, sin, pi, sqrt, simplify
from sympy.matrices import Matrix

### Create symbols for joint variables
# The numbers 1 to 4 correspond to each rotation in the order specified to you.
q1, q2, q3, q4 = symbols('q1:5')

### Define functions for Rotation Matrices about x, y, and z given specific angle.

def rot_x(q):
    R_x = Matrix([[ 1,              0,        0],
                  [ 0,         cos(q),  -sin(q)],
                  [ 0,         sin(q),  cos(q)]])
    
    return R_x
    
def rot_y(q):              
    R_y = Matrix([[ cos(q),        0,  sin(q)],
                  [      0,        1,       0],
                  [-sin(q),        0, cos(q)]])
    
    return R_y

def rot_z(q):    
    R_z = Matrix([[ cos(q),  -sin(q),       0],
                  [ sin(q),   cos(q),       0],
                  [      0,        0,       1]])
    
    return R_z
              
### Define rotations between frames

# Initial Rotation Matrix for Frame A
Ra = Matrix([[1, 0, 0],
             [0, 1, 0],
             [0, 0, 1]])


# Rotations performed on individual Frames for A->B->E
Rb_a = rot_y(q1)
Re_b = rot_x(q2)

# Rotations performed on individual Frames for A->C->D->E
Rc_a = Ra
Rd_c = rot_x(q3)
Re_d = rot_z(q4)

### Define Translations between frames.

tb_a = Matrix([ [-2],  [2], [4]])
te_b = Matrix([  [0],  [2], [0]])
tc_a = Matrix([  [4],  [4], [0]])
td_c = Matrix([ [-3],  [3], [2]])
te_d = Matrix([ [-3],  [2], [3]])

### Define homogenous transformation matrices
Ta = Ra.row_join(Matrix([[0], [0], [0]]))
Ta = Ta.col_join(Matrix([[0, 0, 0, 1]])) 

Tb_a = Rb_a.row_join(tb_a)
Tb_a = Tb_a.col_join(Matrix([[0, 0, 0, 1]]))

Te_b = Re_b.row_join(te_b)
Te_b = Te_b.col_join(Matrix([[0, 0, 0, 1]]))

Tc_a = Rc_a.row_join(tc_a)
Tc_a = Tc_a.col_join(Matrix([[0, 0, 0, 1]]))

Td_c = Rd_c.row_join(td_c)
Td_c = Td_c.col_join(Matrix([[0, 0, 0, 1]]))

Te_d = Re_d.row_join(te_d)
Te_d = Te_d.col_join(Matrix([[0, 0, 0, 1]]))               

### Composition of Transformations
Te_a_1 = simplify(Ta * Tb_a * Te_b)

Te_a_2 = simplify(Ta * Tc_a * Td_c * Te_d)

### Calculate orientation and position for E
E_1 = Te_a_1.evalf(subs={q1: -pi/2, q2: pi/2}, chop = True)

E_2 = Te_a_2.evalf(subs={q3: pi/2, q4: pi/2}, chop = True)

Now what if we needed to explicitly solve for the transform ^C_DT? All that is required is to make use of inverse transforms, applied in the proper order. First, premultiply both sides by ^A_CT^{-1} = ^C_AT and then post-multiply both sides by ^D_ET^{-1} = ^E_DT .